Moving Averages (Moyennes mobiles)
Une moyenne mobile est une méthode permettant de calculer la valeur moyenne des prix d’un titre, ou d’un indicateur, sur une période donnée. Le terme même de " mobile " laisse entendre, et de façon correcte, que la moyenne change ou est en mouvement. Quand vous calculez une moyenne mobile, il est fait une analyse mathématique de la valeur moyenne d’un titre sur une période déterminée. Alors que les prix du titre changent avec le temps, sa moyenne mobile avancera ou reculera.
MetaStock calcule et affiche six sortes de moyennes mobiles : la moyenne simple/simple (autrement appelée arithmétique), exponentielle/exponential, par régression linéaire/time series, triangulaire/triangular, variable/variable, et pondérée/weighted. En plus, MetaStock pourra calculer les moyennes mobiles sur le cours d’ouverture/open d’une valeur, le plus hauts/high, le plus bas/low, la clôture/close, le prix médian/median price, le prix typique/typical price, les volumes/volume, la position ouverte/open interest, ou un indicateur/indicator.
La seule différence significative entre ces formes diverses de moyennes mobiles, ce sont les pondérations qui sont assignées aux observations les plus récentes. Une fois que ce processus de pondération est établi, il restera inchangé sur toute la durée du calcul. Les deux seules exceptions sont la moyenne mobile variable et la moyenne mobile ajustée par les volumes. La moyenne mobile variable ajuste automatiquement sa pondération en fonction des conditions du marché. Une moyenne mobile variable devient plus sensible aux données les plus récentes quand la volatilité augmente, et moins sensibles à ces données les plus récentes lorsque la volatilité décroît. De la même façon, la moyenne mobile ajustée par les volumes s’ajuste automatiquement alors que les volumes échangés sur la valeur s’accroissent ou décroissent.
Voir page pour plus d’informations sur la façon de tracer les indicateurs. Pour plus d’informations sur les paramètres des moyennes mobiles.
Méthodes de calcul de moyennes mobiles
Exponentielle
Une moyenne mobile exponentielle/exponential (ou à pondération exponentielle) est calculée en appliquant un certain pourcentage de la valeur du cours de clôture du jour à la valeur de la moyenne mobile de la veille.
Par exemple, pour calculer une moyenne mobile exponentielle à 9% d’IBM : premièrement, nous prendrons le cours de clôture du jour et le multiplierons par 9%. Nous ajouterons ensuite ce montant à la valeur de la moyenne mobile de la veille que nous multiplierons par 91% (100% - 9% = 91%).
m.m. = [(clôture du jour)
× 0.09] + [(m.m. de la veill.e )× 0.91]C’est parce que la majorité des investisseurs se sentent plus à l’aise à travailler avec des unités de temps plutôt qu’avec des pourcentages que MetaStock convertit les jours en moyennes mobiles exponentielles. Par exemple, si une moyenne mobile exponentielle à 21 jours est requise, le logiciel calculera automatiquement une moyenne mobile à 9%.
La formule permettant de convertir les jours en pourcentage exponentiel est la suivante :
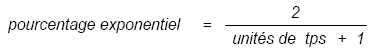
Par exemple, pour calculer une moyenne mobile exponentielle à 10 jours, vous devriez utiliser le coefficient 0.18 :
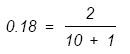
Pour convertir un pourcentage exponentiel en unités de temps, vous devriez utiliser la formule suivante :
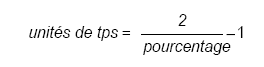
Si on prend l’exemple précédent, on peut vérifier pour voir si une moyenne mobile exponentielle à 0.18 est bien une moyenne mobile à 10 jours.
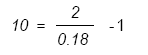
La méthode utilisée pour calculer une moyenne mobile exponentielle place une forte pondération sur les données les plus récentes et une plus faible pondération sur les données les plus anciennes, que ne le fait la méthode de la moyenne mobile simple. Cette dernière méthode est souvent appelée pondération exponentielle.
Simple
Une moyenne mobile simple, ou arithmétique, est calculée en faisant la somme des cours de clôture d’une valeur sur un nombre d’unités de temps données (e.g., 12 days) et puis en divisant ce total par le nombre d’unités de temps. Le résultat est le prix moyen de la valeur sur la période de temps choisie.
Par exemple, pour calculer une moyenne mobile à 21 jours d’IBM : d’abord nous commençons par faire la somme de tous les cours de clôture d’IBM sur les 21 dernières journées. Ensuite, nous divisons cette somme par 21, et cela nous donnera le cours de clôture moyen d’IBM sur les 21 dernières journées. Nous pointerons ensuite ce prix moyen sur le graphique. Le jour suivant (le lendemain) nous reprendrons le même calcul : addition des cours de clôture des 21 dernières journées écoulées, division de cette somme par 21, et pointage du chiffre qui en résulte sur le graphique.
Par régression linéaire
La moyenne mobile par régression linéaire/time series, est utilisée en utilisant la technique des régressions linéaires. Mais au lieu de tracer la ligne droite de régression linéaire, une moyenne mobile de série chronologique pointera le point de terminaison de la ligne. Elle y parvient en utilisant un nombre spécifié d’unités de temps pour chaque journée. Ces points individuels sont ensuite reliés entre eux au travers d’une courbe qui forme la moyenne mobile par régression linéaire.
On fait parfois référence à cette moyenne mobile en parlant d’oscillateur de régression.
Pour plus d’informations sur le calcul de régressions linéaires par la méthode des moindres carrés (autrement dit la base du calcul des moyennes mobiles par régression linéaire), faites appel à n’importe quel ouvrage de statistiques.
Triangulaire
Une moyenne mobile triangulaire/triangular est similaire à une moyenne mobile exponentielle et à une moyenne mobile pondérée à l’exception du système de pondération qui est différent. Les moyennes mobiles exponentielles et pondérées assignent la majeure partie de leur pondération aux données les plus récentes. La moyenne mobile simple assigne une pondération égale à toutes les données utilisées. Avec une moyenne mobile triangulaire, la majorité de la pondération est assignée à la portion médiane des données.
Une moyenne mobile triangulaire est tout simplement une moyenne mobile simple à double lissage. Pour calculer une moyenne mobile triangulaire à 9 unités de temps (et c’est la même chose à chaque fois que le nombre d’unités de temps choisi sera un chiffre impair) suivez les étapes suivantes:
1) Divisez 9 par 2 pour obtenir 4.5
2) Arrondissez à 5
3) Moyenne mobile triangulaire (nbre impair) = (mov(mov(c,5,s)5,s)
Une moyenne mobile triangulaire à 12 unités de temps (et c’est la même chose à chaque fois que le nombre d’unités de temps choisi est un nombre pair) est calculée comme suit :
1) Divisez 12 par 2 pour obtenir 6.
2) Ajoutez 1 à 6 pour obtenir 7
*.3) Moyenne mobile triangulaire (nombre pair) = (mov(mov(c,6,s),7,s)
*
La règle consiste à prendre la longueur que vous divisez par deux pour la première moyenne, et à laquelle vous ajoutez 1 pour la seconde.Une moyenne mobile variable est une moyenne mobile exponentielle qui ajuste automatiquement la constante de lissage en fonction de la volatilité de la série de données. Plus les données sont volatiles, plus la constante de lissage utilisée dans le calcul de la moyenne mobile est grande. Plus la constante de lissage est grande, plus vous donnez de poids aux données les plus récentes. Le raisonnement est inverse pour les données moins volatiles.
Une forte volatilité est souvent associée par les traders à des marchés à forte directionnalité. Ce n’est cependant pas exact. Des marchés à forte directionnalité, ou à tendance marquée, sont moins volatils à cause de l’uniformité des variations de prix d’un jour à l’autre. C’est lorsque les variations de prix d’un jour à l’autre sont erratiques (i.e., forte baisse, petite hausse, petite hausse, forte hausse, petite baisse, etc...), que la volatilité augmente. Ce genre de comportement peut se rencontrer tant sur des marchés à tendance haussière que sur des marchés à tendance baissière que sur des marchés sans tendances.
En règle générale, les moyennes mobiles pâtissent de ne pas pouvoir compenser pour tenir compte des variations de la volatilité. Dans le cadre de marchés volatils, vous aimeriez qu’une moyenne mobile accroisse sa sensibilité à l’action des prix de façon à ce que vous vous retrouviez rapidement dans le bon sens de toute giration brusque et forte. En ajustant constamment sa constante de lissage, une moyenne mobile variable a la possibilité d’ajuster sa sensibilité, ce qui lui permet de donner de meilleurs résultats à la fois sur des marchés à forte et sur des marchés à faible volatilité.
MMV = (0.78*(indice de volatilité) * clôture) + (1-0.078 *indice de volatilité)*MMV de la veille
La valeur absolue du Chande Momentum Oscillator à 9 unités de temps est utilisée pour l’indice de volatilité. Plus l’indice de volatilité est fort et plus le marché est volatil, augmentant de cette façon la sensibilité de la moyenne mobile.
Cette méthode de calcul d’une moyenne mobile variable a été présentée par Tushar Chande dans le numéro de mars 1992 de Technical Analysis of Stocks and Commodities magazine.
Ajustée par les volumes
Dick Arms, renommé surtout pour avoir inventé le Arms Index et la méthode de représentation graphique en équivolume (voir page), a également mis au point une méthode unique de calcul des moyennes mobiles. En restant dans le cadre des recherches basées sur l’utilisation des données de volumes, cette méthode de calcul intègre donc les volumes dans le calcul de moyenne mobile et est appelée moyenne mobile ajustée par les volumes/volume adjusted moving average.
Le calcul d’une moyenne mobile ajustée par les volumes est plutôt complexe ; il est cependant relativement facile à comprendre de façon conceptuelle. Toutes les moyennes mobiles (même celles qui sont ajustées par les volumes) utilisent, sous une forme ou une autre, un procédé permettant de "moyenner" les données. Les moyennes mobiles exponentielles et pondérées attribuent le plus grand poids aux données les plus récentes. Les moyennes mobiles simples attribuent le même poids à toutes les données. Les moyennes mobiles variables attribuent le plus grand poids aux données les plus volatiles. Et comme leur nom l’indique, les moyennes mobiles ajustées par les volumes attribuent le plus grand poids aux journées avec les plus forts volumes.
Une moyenne mobile ajustée par les volumes est calculée de la façon suivante:
1. Calculez les volumes moyens en utilisant toutes les unités de temps du graphique.
2. Calculez l’unité de volumes ou le " volume incrément " en multipliant le volume moyen par 0.67.
3. Calculez le ratio de volumes de chaque unité de temps en divisant les volumes réels de l’unité de temps en question par l’unité de volumes que vous venez de calculer.
4. En partant de l’unité de temps la plus récente et en travaillant en arrière, multipliez le prix de chaque unité de temps par le ratio de volumes de la période et additionnez cumulativement ces valeurs jusqu'à ce que le total atteigne le nombre d’unités de volumes qui sera spécifié par l’utilisateur. Vous remarquerez que seule une portion des volumes de la dernière unité de temps sera probablement utilisée.
Pondérée
Une moyenne mobile pondérée/weighted est bâtie également dans l’idée d’accorder aux données les plus récentes une plus lourde pondération qu’aux données les plus anciennes. Une moyenne mobile pondérée est calculée en multipliant chacune des données des jours qui ont précédé par un coefficient de pondération donné. Le tableau suivant montre comment une moyenne mobile pondérée à 5 jours est calculée.